CC BY 4.0(除特别声明或转载文章外)
soj 1035 –DNA matching
soj 1681 –Matchsticks
soj 1620 –SCVs and minerals
soj 2503 –最长字符串
soj 1783 –Large is Better
soj 8536 –Happy Camper
soj 6771 –Class Packing
题号:soj 1035 --DNA matching
题目:给定n个DNA单链,问最多能组成多少对DNA双链,每一个DNA单链只能使用一次,且不可翻转。两个DNA单链能够形成一对DNA双链的条件是对应位置A/T,C/G配对。(1<=n<=100)
第一段乍一看有点不大好处理,其实可以利用数组来解决对应位配对的情况!而对于整体的求解,类似于遍历去找配对的一对对,只不过这里是读入数据时便确定了配对情况:与集合里已有的DNA若可配对则计数+1,否则将读入的DNA装进待配对集合里。
#include <set>
int matching(int n){
static char match_str[127];
match_str['A'] = 'T';
match_str['T'] = 'A';
match_str['G'] = 'C';
match_str['C'] = 'G';
int matchNum = 0;
multiset<string> S;
string str, matchedStr;
for (int i = 0; i < n; ++i){// n条DNA
cin >> str;
matchedStr = "";
for (int j = 0; j < str.size(); ++j){
matchedStr += match_str[str[j]];
}
if (S.count(matchedStr)){
++ matchNum;
S.erase(S.lower_bound(matchedStr));
}
else {
S.insert(str);
}
}
return matchNum;
}
题号:soj 1681 --Matchsticks
题目:如下图所示,给定n根火柴,求其可以摆出的最小的数和最大的数(2<=n<=100)
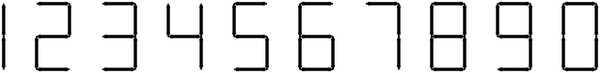
显然,由于数字1只需要2根火柴以及数字7只需要3根火柴,最大的数必然全为1(偶数根火柴)或打7开头后全为1(奇数根火柴)。
而对于最小的数,先枚举火柴数少的情况,再通过递归对火柴数更多的情况进行选择。
string minNum(int matchsticks){//不喜用switch-case语句
if (matchsticks == 2) return "1";
else if (matchsticks == 3) return "7";
else if (matchsticks == 4) return "4";
else if (matchsticks == 5) return "2";
else if (matchsticks == 6) return "6";
else if (matchsticks == 7) return "8";
else if (matchsticks == 8) return "10";
else if (matchsticks == 10) return "22";
else {
string min1= minNum(matchsticks - 7) + "8";
string min2 = minNum(matchsticks - 6) + "0";
if (min1.size() < min2.size() || min1 < min2) return min1;
else return min2;
}
}
string maxNum(int matchsticks){
string tmp = "";
if (matchsticks % 2 == 0) {
for (int i = 0; i < matchsticks/2; ++i) {
tmp += "1";
}
}
else {
tmp = "7";
matchsticks -= 3;
for (int i = 0; i < matchsticks / 2; ++i) {
tmp += "1";
}
}
return tmp;
}
此题有两个坑:1. 题目要求”no leading zeroes”,这里也包括了一位数的情况,即给定6根火柴棒时最小数不取0。 2. 虽然火柴数为9的情况可以由递归解决但为10时不可,所以也需另外给出。
题号:soj 1620 --SCVs and minerals
题目:游戏“ StarCraft”设定为,最初您有N个SCV和M个mineral。每个SCV可以在一秒钟内获得C个mineral,而指挥中心可以立即用P个mineral生产1个SCV。求在S秒后可获得的最多的mineral数量。
最开始的想法就是递归调用,想在每一步都得到最多的mineral。样例输出很快否定了这个方法,仔细一想才发现,这个问题可以转换成我们熟悉的场景——生意买卖,只要作为生产设备的SCV能够在剩下的时间内产出不少于成本价P的mineral,那么赚得的肯定就最多了。
#include <iostream>
using namespace std;
int main() {
int testNum = 0;
cin >> testNum;
for (int i = 0; i < testNum; ++i) {
int N, M, C, P, S;
cin >> N >> M >> C >> P >> S;
for (int j = 0; j < S; ++j) {
if ((S - j) * C >= P) {//P是获得一个SCV的成本,(S-j)*C是该SCV能带来的收入
N += M / P;
M %= P;
}
M += N * C;
}
cout << M << endl;
}
}
题号:soj 2503 --最长字符串
题目:要求你构造一个由字符'A','B'组成的字符串, 满足以下几个条件:
1) A的个数<=countA
2) B的个数<=countB
3) 连续的A的个数不可以超过maxA.
4) 连续的B的个数不可以超过maxB.
5) 这个字符串的长度最长.
给定countA, countB, maxA, maxB, 求输出字符串的最大长度。
不知道是不是被算法名字所束缚了,总想着在每一步都积累最多的’A’或’B’以求整体最大,这个想法最大的漏洞在于:两者的数量差可能是悬殊的,这个时候尽可能更多地分组才是最优解。
此题解法:将A或B作为基准,另外一个进行分组作为分隔符。如果非分隔符多于分组数量,尽可能填满分隔符之间的空隙;若分组数量多于非分隔符,则尽可能填充更多的空隙。
#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
int handler(int countA, int countB, int maxA, int maxB) {//以A为基准,以B为分隔符
if (maxA == 0) return min(maxB, countB);
if (maxB == 0) return min(maxA, countA);
int despNum = ceil(countB / maxB);//ceil()向上取整,即前n-1组B的数量同,最后一组可能不同
if (countA > despNum) return min(countA + countB, countB + (despNum + 1) * maxA);
else return countA + min(countB, (countA+1)*maxB);
}
int main() {
int countA, countB, maxA, maxB;
cin >> countA >> countB >> maxA >> maxB;
int len1 = handler(countA, countB, maxA, maxB);
int len2 = handler(countB, countA, maxB, maxA);
cout << max(len1, len2) << endl;
}
题号:soj 1783 --Large is Better
题目:给定一个数字,除了0,可以交换任意数量的相邻数字,不允许用数字0去交换任何数字。求经过交换所能得到的最大数字。
没有太大难度,就是分割排序。不过用迭代器这个骚操作真得学起来了啊…
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main() {
int testNum;
cin >> testNum;
while (testNum--) {
string str1;
cin >> str1;
int length = str1.size();
if (length == 1) {
cout << str1 << endl;
continue;
}
//进一步优化:用iterator去指向每个分割的部分
string::iterator iter1 = str1.begin();
string::iterator iter2 = iter1;
for (int i = 0; i < length; ++i) {
if (*iter2 == '0') {
sort(iter1, iter2, greater<>());
iter1 = iter2+1;
}
++iter2;
}
sort(iter1, iter2, greater<>());
cout << str1 << endl;
}
}
题号:soj 8536 --Happy Camper
题目:设整数1<L<P<V,在任何连续的P天时间里,露营地的占用限于L天。Harry Camper拥有V天的假期。请问假期期间,他最多可以露营地住多少天?
不知道为什么这么简单的题目会被放进课件里…就是分割啦跟上上道题同源的思想然而比那个水好多…
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int L, P, V;
int caseNum = 1;
while (cin >> L >> P >> V) {
if (!(L && P && V)) return 0;
int maxDays = 0;
int despNum = V / P;
maxDays += L * despNum;
if (despNum * P < V) {
maxDays += min(L, V - despNum * P);
}
cout << "Case " << caseNum << ": " << maxDays << endl;
++caseNum;
}
}
题号:soj 6771 --Class Packing
题目:年级为0~6共七个年级的学生,给定每个年级的学生数量。现为这些学生分配班级,需要满足以下条件:
1:一个班级只能有一个年级或两个相邻年级的学生,例如,四年级和五年级学生的班级人数不得超过25。
2: 拥有年级0-2的学生的班级,其人数最多为20。
3: 拥有年级3-4的学生的班级,其人数最多为25。
4: 拥有年级5-6的学生的班级,其人数最多为30。
求至少需要分配多少个班级。
emmm…看提示之前是思绪是非常乱的…纠结于how to divide them…Fine其实正确思路再简单不过了:如果人数多的话,将他们尽量分配到同一个班的结果是理想的(因为如果分配到其他的班,可能会影响到高年级的班级的容量);如果人数有剩下的话,就从其上一年级中调派人员过来,使得该班的容量填满。
#include <iostream>
using namespace std;
int main() {
int grade[7];
while (cin >> grade[0] >> grade[1] >> grade[2] >> grade[3] >> grade[4] >> grade[5] >> grade[6]) {
bool flag = true;
for (int i = 0; i < 7; ++i) {
if (grade[i] != 0) {
flag = false;
break;
}
}
if (flag) return 0;
int limits[7] = { 20, 20, 20, 25, 25, 30, 30 };
int num = 0;
int left = 0;
for (int i = 0; i < 7; ++i) {
while (grade[i] > 0) {
if (left != 0 && grade[i-1] < 0) {
grade[i] -= left;
left = 0;
continue;
}
if (grade[i] < limits[i]) {
left = limits[i] - grade[i];
}
++num;
grade[i] -= limits[i];
}
}
cout << num << endl;
}
}
🐣最后一点点想法:C++标准库函数真的很实用!
(未完待续)
附录:
