CC BY 4.0(除特别声明或转载文章外)
soj 1121 –Tri Tiling
soj 1264 –Atomic Car Race
soj 1828 –Minimal
soj 1527 –Tiling a Grid With Dominoes
soj 1148 –过河
soj 1163 –Tour
soj 1345 –能量项链
soj 1687 –Permutation
题号:soj 1121 --Tri Tiling
题目:用1*2的长方形铺满3*n的长方形,有多少种方法?(如下图)
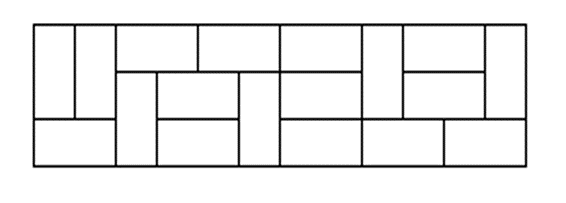
初始状态,n=2时,可以平铺出矩形(3种情况)和非矩形(2种情况),如下图所示。
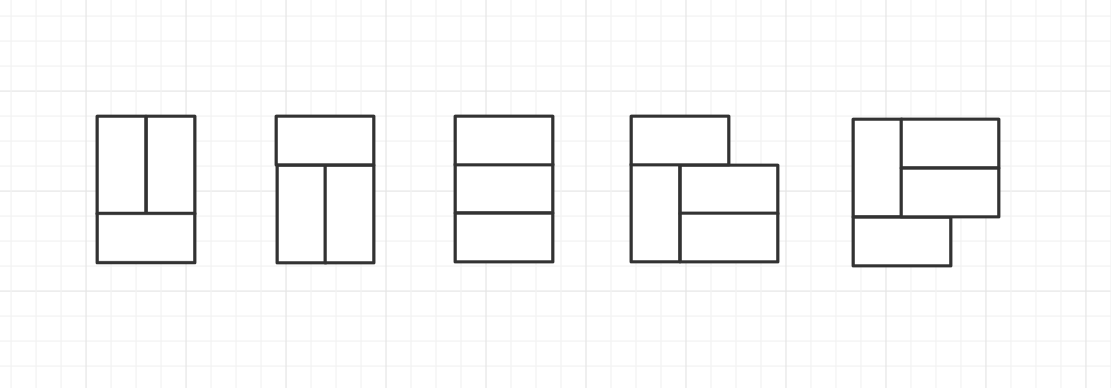
题解一:用f[i]表示铺满3 * (2i)的长方形的方案数,用g[i]表示铺满3 * (2i)的长方形,并且向后伸展出部分形状的方案数。则有:
- f[i]=3*f[i-1]+g[i-1]
3 * f[i-1]即在f[i-1]的基础上要加上恰好的3 * 2矩形才能构成f[i],而3 * 2矩形有3种情况(如上图);g[i-1]即对于每一种非矩形都只有一种方式可以填补其使之恰为矩形。
- g[i]=2*f[i-1]+g[i-1]
2 * f[i-1]即在f[i-1]的基础上要加上2种非矩形之一才能构成g[i];g[i-1]即对于每一种非矩形都只有一种方式可以填补其使之恰为非矩形。
#include <iostream>
using namespace std;
const int maxn = 32;
int f[maxn], g[maxn];
int dp(int n) {
if (n % 2 == 1) return 0;
if (n == 0) return f[0] = 1;
f[1] = 3;
g[1] = 2;
int tmp = n / 2;
for (int i = 2; i <= tmp; ++i) {
f[i]=3*f[i-1]+g[i-1];
g[i]=2*f[i-1]+g[i-1];
}
return f[tmp];
}
int main() {
int n;
while (cin >> n && n != -1) {
cout << dp(n) << endl;
}
}
题解二:数学规律推算法
要使3*n是一个矩形,有两种可能:
1. 3*(n-2)也是一个矩形,那么只要再拼上一个3*2的就可以了。这个3*2有3种情况,所以是3*f(n-2);
2. 3*(n-2)不是一个矩形,这种情况下,你只有一种添加2*1块的方法使得3*n是矩形,还需要对3*(n-4)的形状做判断:
1. 3*(n-4)是一个矩形,那么只要再拼一个L形或者倒L形就可以使得3*(n-2)不是矩形了,这里就是2*f(n-4);
2. 3*(n-4)不是一个矩形,那么也是只有一种添加2*1块的方法能使3*(n-2)不是矩形,接下来就来考虑3*(n-6):
1. 3*(n-6)是一个矩形,那么只要再拼一个L形或者倒L形就可以使得3*(n-4)不是矩形了,这里就是2*f(n-6);
2. 3*(n-6)不是一个矩形,……
综上,可以得到递推式:f(n) = 3 * f(n-2) + 2 * f(n-4) + 2 * f(n-6) + … + 2 * f(0),其中初始值f(0)=1。
#include <iostream>
using namespace std;
const int maxn = 30;
int f[maxn] = {0};
int dp(int n) {
if (n % 2 == 1) return 0;
if (n == 0) return f[0] = 1;
if (n == 2) return f[2] = 3;
if (f[n] != 0) return f[n];
f[n] += 3 * dp(n - 2);
for (int i = 2; i <= n/2; ++i) {
f[n] += 2 * dp(n - 2 * i);
}
return f[n];
}
int main() {
int n;
while (cin >> n && n != -1) {
cout << dp(n) << endl;
}
}
题号:soj 1264 --Atomic Car Race
题目:在一次赛车比赛中,共有n个检查点,在每个检查点可以选择是否更换轮胎,更换轮胎需要花费b秒。在一次更换轮胎之后,赛车的速度先增加(轮胎变热),后减少(轮胎损坏),每公里行驶需要的时间可以表达为(x为当前检查点与最近一次更换轮胎的检查点的距离,从x公里跑到x+1公里):
1/(v - e * (x - r)) (if x >= r)
1/(v - f * (r - x)) (if x < r)
求从起点到终点需要耗费的最少时间。
限制:
· 0 < n <= 100
· 0 <= r <= an-1
· 0 < a1 < a2 < … < an <= 10000
· v – e * (x - r)>=0.01
· v - f * r >= 0.01
好难啊…总是不容易想到用辅助数组的。
这里主要维护两个数组,先看辅助数组 cost[k] (0 <= k <= an),抛开对最优解的思考,它表示距离上一次换轮胎已连续行驶了 k 公里耗费的总时间,由于换轮胎之后的用时与换之前的状态无关,所以我们可以推出:
- cost[k] = 0
- cost[k] = cost[k-1] + T(k-1)
其中,T(k-1)表示更换轮胎后从第 k-1 公里处行驶至第 k 公里处消耗的时间,由题目可知
- 当 k < r 时,T(k-1) = 1/(v-f*(r-(k-1)))
- 当 k >= r 时,T(k-1) = 1/(v-e*((k-1)-r))
接下来我们思考要求解的问题。用数组 dp[i] 表示从起点到达第 i 个检查点所用的最短时间。
对于一个最优解,假设在这个最优解中行驶到第 j 个检查点完成了最后一次换轮胎,则有 dp[n] = dp[j] + cost[an - aj] + b。
那么dp[i]的递推式即为:dp[i] = min(dp[0] + cost[ai - a0] + b, dp[1] + cost[ai - a1] + b…dp[i-1] + cost[ai - ai-1] + b)。
需要注意的是,Sicily对该题目的输出有精度要求,故使用流操作符 fixed 来使浮点输出应该以小数点表示法显示。
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int n;
while (cin >> n && n != 0) {
int a[10001];
a[0] = 0;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
}
double b, r, v, e, f;
cin >> b >> r >> v >> e >> f;
double cost[10001];
cost[0] = 0;
for (int i = 1; i <= a[n]; ++i) {
cost[i] = i - 1 < r ? cost[i - 1] + 1 / (v - f * (r - i + 1)) : cost[i - 1] + 1 / (v - e * (i - 1 - r));
}
double dp[10001];
dp[0] = 0;
for (int i = 1; i <= n; ++i) {
double min_time = dp[0] + cost[a[i]];
for (int j = 1; j < i; ++j) {
min_time = min(min_time, dp[j] + cost[a[i] - a[j]] + b);
}
dp[i] = min_time;
}
cout << fixed << dp[n] << endl;
}
return 0;
}
题号:soj 1828 --Minimal
题目:There are two sets S1 and S2 subjecting to:
(1) S1, S2 are both the subsets of {x| x is an integer and 0 < x < 1,000,000}
(2) 0 < |S1| < |S2| < 500
F(S1, S2) = min {|a1-b1| + |a2-b2| + … + |aN-bN|} in which ai ∈S1, bi ∈S2, ai ≠aj if i≠j, bi ≠bj if i≠j (i, j = 1, 2 … N,N = |S1|)
For each test case, print the result of F(S1 ,S2).
最开始我的想法是,将S1和S2作笛卡尔积(定义X为两数差距),在一个二维数组里记录两两之差的绝对值,对S1每个元素都匹配以S2某个元素使得差距尽可能小。尝试了几个测例都过了,但是OJ上面WA了,这个解法个人觉得也有些牵强,无法证明,但又无法证伪😭。
假设我们从S2中选择了某些数,假设选出的数组成S3,那么S3中最小的数肯定匹配S1中最小的数,S3中次小的数匹配S1中次小的数…
证明:
假设S1中有了a1,a2,S3中有b1,b2
且a1<=a2,b1<=b2
那么有|a1-b1|+|a2-b2|<=|a1-b2|+|a2-b1|(数学问题)
所以从小到大一个个匹配不会更差,只会更好。
解法:
对S1和S2分别从小到大排序,用f[i][j]表示S1中的前i个数,与S2中的前j个数匹配(从j个数选i个数出来),显然有:
f[i][j] = inf(j < i)
f[0][0] = 0
f[i][j] = min{f[i-1][j-1]+|a[i]-b[j]|,f[i][j-1]},j>=i
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
#define inf 1<<30
const int maxn = 501;
int f[maxn][maxn];
int S1[maxn], S2[maxn];
int main() {
int cases;
cin >> cases;
while (cases--) {
int N, M;
cin >> N >> M;
for (int i = 1; i <= N; ++i) {
cin >> S1[i];
}
for (int i = 1; i <= M; ++i) {
cin >> S2[i];
}
sort(S1+1, S1+N+1);
sort(S2+1, S2+M+1);
for (int i = 0; i <= N; ++i) {
for (int j = 0; j <= M; ++j) {
if (i == 0 && j == 0)
f[i][j] = 0;
else if (i > j) {
f[i][j] = inf;
}
else {
f[i][j] = inf;
if (i > 0)
f[i][j] = min(f[i][j], f[i-1][j-1]+abs(S1[i]-S2[j]));
if (j > 0)
f[i][j] = min(f[i][j], f[i][j-1]);
}
}
}
cout << f[N][M] << endl;
}
}
题号:soj 1527 --Tiling a Grid With Dominoes
题目:用1*2的长方形铺满4*n的长方形,有多少种方法?(如下图)
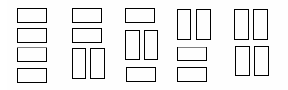
处理方式与上题有些相似,但思路有所不同:用f[i][j]表示前4*i列已经完全填满,并且第(i+1)列情况为第j种形状的方案数。其中,共有5种形状,分别是:
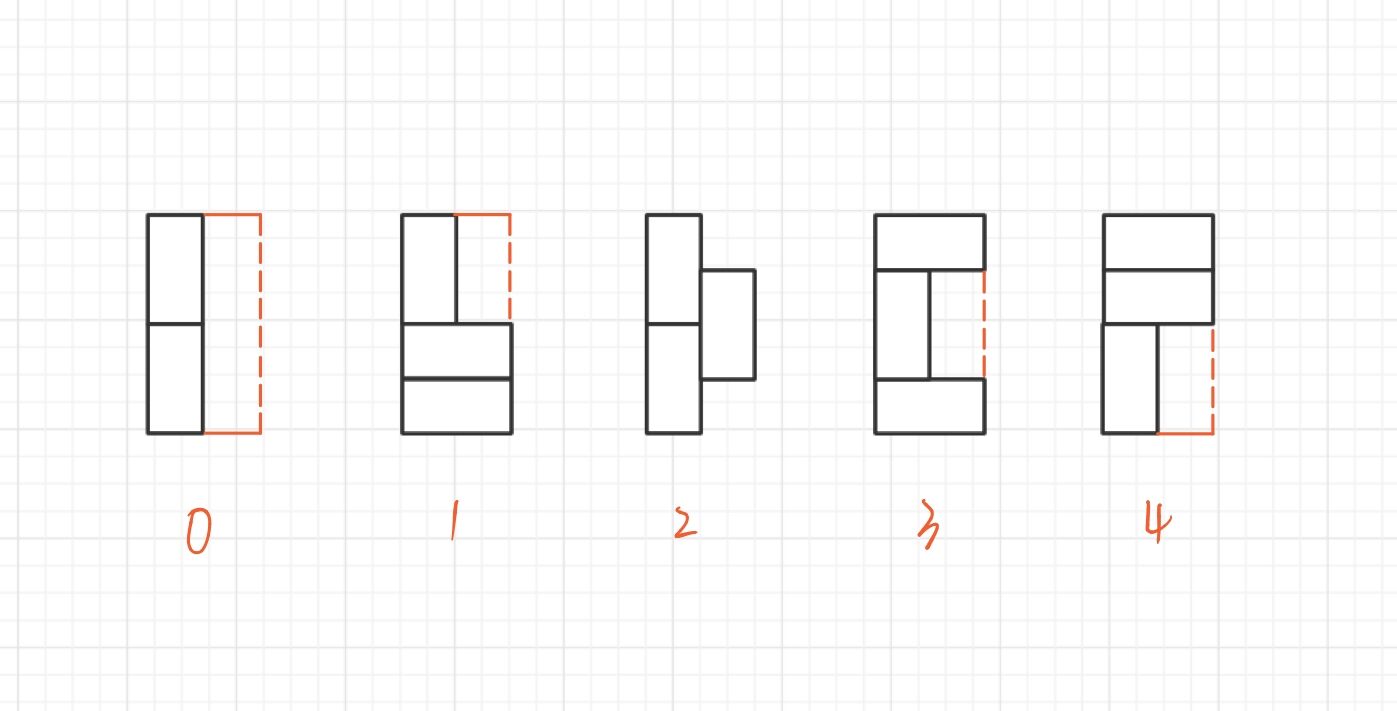
#include <iostream>
using namespace std;
const int maxn = 1001;
int f[maxn][5];
int dp(int N) {
f[0][0] = f[1][0] = f[1][1] = f[1][3] = f[1][4] = 1;
f[1][2] = 0;
for (int i = 2; i <= N; ++i) {
f[i][0] = f[i-2][0]+f[i-1][0]+f[i-1][1]+f[i-1][3]+f[i-1][4];
f[i][1] = f[i-1][0]+f[i-1][4];
f[i][2] = f[i-1][3];
f[i][3] = f[i-1][0]+f[i-1][2];
f[i][4] = f[i-1][0]+f[i-1][1];
}
return f[N][0];
}
int main() {
int cases;
cin >> cases;
for (int i = 1; i <= cases; ++i) {
int N;
cin >> N;
cout << i << " " << dp(N) << endl;
}
}
题号:soj 1148 --过河
题目:在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0,1,……,L(其中 L 是桥的长度)。坐标为0的点表示桥的起点,坐标为L的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是 S 到 T 之间的任意正整数(包括S, T)。当青蛙跳到或跳过坐标为L的点时,就算青蛙已经跳出了独木桥。
给定独木桥的长度 L,青蛙跳跃的距离范围 S、T ,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
限制:
· 1 <= L <= 10^9
· 1 <= S <= T <= 10
· 1 <= M < = 100
用数组 $dp[i]$ 表示走到位置 $i$ 至少需要踩到的石子数,易得 $dp[i] = min(dp[i-j])(S <= j <=T)$。因为只要青蛙跳到或跳过坐标为L的点时就算已经跳出独木桥,所以最终结果落在$[dp[L], dp[L+T-1]]$的范围内。
本题更为关键的一点是,L 的范围比较大,直接开长度为 L 的数组几乎不可能,所以要进行状态压缩来达到节省空间的目的。从题目限制来看,S 和 T 比较小,当两个石子之间的距离相对大时,总可以从前一个石子跳到后一个石子,而中间的路程便可以舍去不计。
那么该压缩多少?先从最简单的想起,假如一次只能走 S 或者 T 步,从原点开始走,那么显然一定可以走到LCM(S,T)这个位置。在这种情况下,如果(0, LCM(S,T)]之间没有石子,那么(0,LCM(S,T)]就是无用的,因为它不会对答案产生任何影响,可以把这一段删去。
推广一下就可以知道,从点 i 开始,一次走[S, T]步,一定可以到达 i + LCM(S…T)这个点,利用这个结论,就可以对两点之间的距离进行缩短。
为了免去对 LCM 的计算,直接取100代替 LCM 对距离进行压缩。
#include <iostream>
#include <algorithm>
using namespace std;
int stones[102];
int f[10200] = { 0 };
int dp[10200];
int main() {
int L, S, T, M;
cin >> L >> S >> T >> M;
int result = 0;
if (S == T) {
for (int i = 1; i <= M; ++i) {
int temp;
cin >> temp;
if (temp % S == 0) ++result;
}
}
else {
stones[0] = 0;
for (int i = 1; i <= M; ++i) {
cin >> stones[i];
}
sort(stones + 1, stones + M + 1);
for (int i = 1; i <= M; ++i) {// 状态压缩
if (stones[i] - stones[i-1] > 99) {
int dis = stones[i] - stones[i - 1] - 99;
for (int j = i; j <= M; ++j) {
stones[j] -= dis;
}
}
f[stones[i]] = 1;
}
dp[0] = 0;// 走到位置i需要踩到的最小石子数
for (int i = 1; i <= stones[M] + T; ++i) {
if (i - S < 0) {
dp[i] = -1;
continue;
}
dp[i] = 200;
for (int j = S; j <= T; ++j) {
if (i - j >= 0 && dp[i - j] != -1) dp[i] = min(dp[i - j], dp[i]);
}
if (f[i]) ++dp[i];
}
result = dp[stones[M]];
for (int i = stones[M] + 1; i <= stones[M] + T; ++i) {
result = min(dp[i], result);
}
}
cout << result << endl;
return 0;
}
题号:soj 1163 --Tour
题目:飞行员John Doe喜欢旅行。度假时,他租了一架小飞机,开始游览美丽的地方。为了节省金钱,约翰必须确定连接他的目的地的最短封闭路线。每个目的地由平面中的一个点表示。John使用以下策略:他从最左边的点开始,然后严格地从左到右转到最右边的点,然后他严格地从右边回到起点。已知这些点具有不同的x坐标。
给定平面中的n个点,根据John的策略计算连接这些点的最短闭合行程。
显然从左到右再从右到左的并不方便思考,不如看作是“有两个人均从最左边的点出发,沿着两条不同的路径走,直到其中一个人走到了最右边的点,并且除了起点外其他每个点都恰好被一个人经过”,这样,可以用 dp[i][j] 表示两人分别走到了第 i 个点和第 j 个点后剩下的最小总路程。始终规定:i < j,并且前 j 个点都已经有人经过了。可得状态转移方程:$dp[i][j] = min(dp[i][j+1] + Distance{{p{j}}}{{p{j+1}}}, dp[j+1][j] + Distance{{p{i}}}{{p{j+1}}})$,两人次序对结果没有影响,所以$dp[j+1][j] = dp[j][j+1]$,确保数组格式。
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <cmath>
using namespace std;
double dp[100][100];
double dist[100][100];
int main() {
int N;
while (cin >> N) {
int points[100][2];
for (int i = 1; i <= N; ++i) {
cin >> points[i][0] >> points[i][1];
}
for (int i = 1; i <= N; ++i) {
for (int j = i + 1; j <= N; ++j) {
dist[i][j] = sqrt(pow(points[i][0] - points[j][0], 2) + pow(points[i][1] - points[j][1], 2));
}
}
for (int j = N; j >= 2; --j) {
for (int i = 1; i < j; ++i) {
if (j == N) dp[i][j] = dist[i][j];
else dp[i][j] = min(dp[i][j + 1] + dist[j][j + 1], dp[j][j + 1] + dist[i][j + 1]);
}
}
cout << fixed << setprecision(2)<< dp[1][2] + dist[1][2] << endl;
}
return 0;
}
题号:soj 1345 --能量项链
题目:在Mars星球上,每个Mars人都随身佩带着一串能量项链。在项链上有N颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是Mars人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,则聚合后释放的能量为 m*r*n(Mars单位),新产生的珠子的头标记为m,尾标记为n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设N=4,4颗珠子的头标记与尾标记依次为(2,3) (3,5) (5,10) (10,2)。我们用记号⊕表示两颗珠子的聚合操作,(j⊕k)表示第j,k两颗珠子聚合后所释放的能量。则第4、1两颗珠子聚合后释放的能量为:
(4⊕1)=10*2*3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为
((4⊕1)⊕2)⊕3)=10*2*3+10*3*5+10*5*10=710。
限制:
· 4 <= N <= 100
· 每个输出都是一个正整数E(E ≤ 2.1*10^9)
暂时把环看成链,用 $f[i][j]$ 表示从第 $i$ 个珠子聚合到第 $j$ 个珠子所释放的总能量。易得状态转移方程:
由于项链是一个环形,聚合总可以从链的后部绕回到链的前部,所以还要考虑环的处理。
我的想法是对下标进行取模处理并且当聚合跨越尾部和首部时进行再分割讨论,本质上仍然是环,代码量相对另一种方法多一点。
官方则采用了破环为链的方法,具体做法是把链扩充到原来的两倍长,把前半部分复制到后半部分,在长度为 2 * N 的链上直接作链的思考。
为了代码更加可懂多创建了数组energy[][]表示珠子头尾。
//破环为链
#include <iostream>
#include <algorithm>
using namespace std;
int f[202][202] = { 0 };
int main() {
int N;
while (cin >> N) {
int pearl[101] = { 0 };
for (int i = 1; i <= N; ++i) {
cin >> pearl[i];
}
int energy[202][2];
for (int i = 1; i < N; ++i) {
energy[i + N][0] = energy[i][0] = pearl[i];
energy[i + N][1] = energy[i][1] = pearl[i + 1];
}
energy[N][0] = energy[2 * N][0] = pearl[N];
energy[N][1] = energy[2 * N][1] = pearl[1];
//数组定义在main函数外,每次执行要重置f[][]以覆盖之前的数据,否则出错
for (int i = 1; i <= 2 * N; ++i) {
for (int j = 1; j <= 2 * N; ++j) {
f[i][j] = 0;
}
}
for (int len = 2; len <= N; ++len) {
for (int start = 1; start + len <= 2 * N; ++start) {
int end = start + len - 1;
for (int mid = start; mid < end; ++mid) {
f[start][end] = max(f[start][end], f[start][mid] + f[mid + 1][end] + energy[start][0] * energy[mid][1] * energy[end][1]);
}
}
}
int result = 0;
for (int i = 1; i <= N; ++i) {
result = max(result, f[i][i + N - 1]);
}
cout << result << endl;
}
return 0;
}
//非破环为链
#include <iostream>
#include <algorithm>
using namespace std;
int f[101][101] = { 0 };
int N;
int energy[101][2];
int dp(int start, int end) {
if (start == end) return 0;
if (f[start][end] != 0) return f[start][end];
f[start][end] = 0;
if (start < end) {
for (int k = start; k < end; ++k) {
f[start][end] = max(f[start][end], dp(start, k) + dp(k + 1, end) + energy[start][0] * energy[k][1] * energy[end][1]);
}
}
else {
for (int k = start; k <= N; ++k) {
f[start][end] = max(f[start][end], dp(start, k) + dp(((k + 1) > N ? k + 1 - N : k + 1), end) + energy[start][0] * energy[k][1] * energy[end][1]);
}
for (int k = 1; k < end; ++k) {
f[start][end] = max(f[start][end], dp(start, k) + dp(k + 1, end) + energy[start][0] * energy[k][1] * energy[end][1]);
}
}
return f[start][end];
}
int main() {
while (cin >> N) {
int pearl[101] = { 0 };
for (int i = 1; i <= N; ++i) {
cin >> pearl[i];
}
for (int i = 1; i < N; ++i) {
energy[i][0] = pearl[i];
energy[i][1] = pearl[i + 1];
}
energy[N][0] = pearl[N];
energy[N][1] = pearl[1];
//数组定义在main函数外,每次执行要重置f[][]以覆盖之前的数据,否则出错
for (int i = 1; i <= N; ++i) {
for (int j = 1; j <= N; ++j) {
f[i][j] = 0;
}
}
f[N][1] = energy[N][0] * energy[1][0] * energy[1][1];
int result = 0;
for (int i = 1; i <= N; ++i) {
if (i == 1) result = max(result, dp(i, i + N - 1));
else result = max(result, dp(i, (i + N - 1) % N));
}
cout << result << endl;
}
return 0;
}
题号:soj 1687 --Permutation
题目:众所周知,对n个数进行排列得到的序列数目为 n!。
例如,1 2 3 4 5 和 1 3 5 4 2 都是 5-permutations。
如果我们在每对连续数字之间插入符号“ < ”或“ > ”,则可以获得带有符号的排列。
例如,可以将 1 2 3 4 5 写成 1 < 2 < 3 < 4 < 5, 1 3 5 4 2 可以写成 1 < 3 < 5 > 4 > 2。
请计算带有 k 个“ < ”符号的n-permutations的数量。对结果取模2007。
限制:
· 1 <= n, k <= 100
假设我们已经对长度为 i - 1 的序列的“ < ”数目进行计算了,现在遍历到第 i 个数,即数字 i ,显然数字 i 比当前序列中所有的数都大,那么把数字 i 插进当前序列便有两种情况:
- 当前序列的 i - 1 个数中有 j 个“ < ”: 为使插进数字 i 后 “ < ”数目保持不变,可以在序列的开头插入,或者在当前序列的“ < ”的位置插入,此时共有 j + 1 种选择。
- 当前序列的 i - 1 个数中有 j - 1 个“ < ”: 为使插进数字 i 后 “ < ”数目加一,可以在序列的末尾插入,或者在当前序列的“ > ”的位置插入,此时共有 i - 2 - (j - 1) + 1 = i - j 种选择。
用数组 dp[i][j] 表示长度为 i 且“ < ”个数为 j 的序列的数目,则有递推式:dp[i][j] = dp[i-1][j-1] * (i - j) + dp[i-1][j] * (j + 1)。
比较巧妙的一个处理是,由于一次测试中可能会有多个测例,而给定的 n 和 k 又比较小,故而把动态规划的过程放在了输入 n, k 的循环体之外来避免存在多个测例时的重复计算。
另外,在main函数中好像不能定义太大的数组,会导致堆栈溢出?总之把它放在main函数外面了。
#include <iostream>
using namespace std;
int dp[101][101] = { {0} };
int main() {
int n, k;
dp[1][0] = 1;
for (int i = 2; i <= 101; ++i) {
dp[i][0] = 1;
for (int j = 1; j < i; ++j) {
dp[i][j] = (dp[i - 1][j - 1] * (i - j) + dp[i - 1][j] * (j + 1)) % 2007;
}
}
while (cin >> n >> k) {
cout << dp[n][k] << endl;
}
return 0;
}
(未完待续)
