📝题目

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

注意：你不能倾斜容器，且 n 的值至少为 2。

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

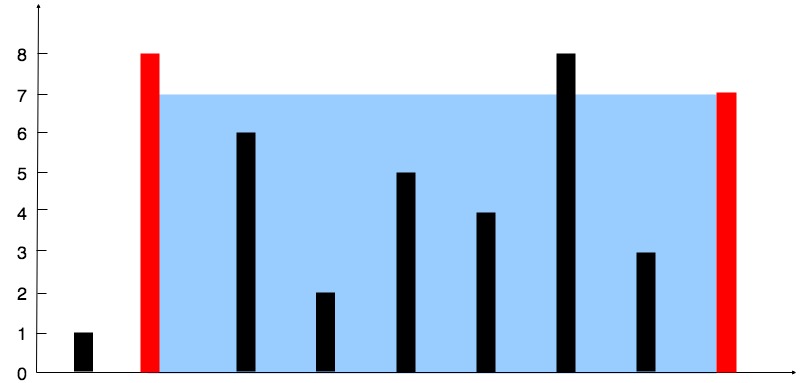
📝思路

暴力的解法三两分钟写了出来，提交上去后超时了…超…时了…了…
官方双指针思路：一开始两个指针一个指向开头一个指向结尾，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，在这种情况下想要让容器盛水变多，就只有在容器的高上下功夫。 那我们该如何决策哪个指针移动呢？我们能够发现不管是左指针向右移动一位，还是右指针向左移动一位，容器的底都是一样的，都比原来减少了1。这种情况下我们想要让指针移动后的容器体积增大，就要使移动后的容器的高尽量大，所以我们选择指针所指的高较小的那个指针进行移动，这样我们就保留了容器较高的那条边，放弃了较小的那条边，以获得有更高的边的机会。
🐣：（一开始我还觉得双指针还能咋用啊不就是跟暴力法一样控制个边而已吗打扰了原来有更进一步考虑（全个想无🙇‍♀️

📝题解

//O(n^2)

int maxArea(vector<int>& height) {
    int len = height.size();
    int max = 0;
    for (int i = 0; i < len-1; ++i){
        for (int j = i+1; j < len; ++j){
            int sum = (height[i] < height[j] ? height[i]*(j-i) : height[j]*(j-i));
            max = max > sum ? max : sum;
        }
    }
    return max;
}

//O(n)

int maxArea(vector<int>& height) {
    int len = height.size();
    int max = 0;
    int left = 0, right = len-1;
    while (left < right){
        int sum = (height[left] < height[right] ? height[left]*(right-left) : height[right]*(right-left));
        max = max > sum ? max : sum;
        if (height[left] < height[right])   ++left;
        else --right;
    }
    return max;
}