CC BY 4.0(除特别声明或转载文章外)
📝题目
在一个火车旅行很受欢迎的国度,你提前一年计划了一些火车旅行。在接下来的一年里,你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。
火车票有三种不同的销售方式:
· 一张为期一天的通行证售价为 costs[0] 美元;
· 一张为期七天的通行证售价为 costs[1] 美元;
· 一张为期三十天的通行证售价为 costs[2] 美元。
通行证允许数天无限制的旅行。 例如,如果我们在第 2 天获得一张为期 7 天的通行证,那么我们可以连着旅行 7 天:第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。
返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。
示例 1:
输入:days = [1,4,6,7,8,20], costs = [2,7,15]
输出:11
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 1 天生效。
在第 3 天,你花了 costs[1] = $7 买了一张为期 7 天的通行证,它将在第 3, 4, ..., 9 天生效。
在第 20 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 20 天生效。
你总共花了 $11,并完成了你计划的每一天旅行。
示例 2:
输入:days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出:17
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[2] = $15 买了一张为期 30 天的通行证,它将在第 1, 2, ..., 30 天生效。
在第 31 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 31 天生效。
你总共花了 $17,并完成了你计划的每一天旅行。
限制:
· 1 <= days.length <= 365
· 1 <= days[i] <= 365
· days 按顺序严格递增
· costs.length == 3
· 1 <= costs[i] <= 1000
📝思路
主干思路:
- 今天不需要出门,不用买票
- 今天如果要出门,需要买几天?
- 看往后几天(最多30天内)要不要出门
- 30天内都没有要出行的,那只买今天就好
- 有要出门的(不同决策)
- 这次 和 后面几次 分开买更省
- 这次 和 后面几次 一起买更省
- 看往后几天(最多30天内)要不要出门
上述思路显而易见,最关键在于:「今天买多少,得看后几天怎么安排」,即「前面依赖后面」——从后向前来买。
如图所示,例如:$days = [1,4,6,7,8,20]$
- 第 21 及以后的日子都不需要出门,不用买票
- 第 20 需要出门,需要买几天?
- 不考虑 20 之前要不要出门,否则与思路相违背
- 第 20 之后没有出门日,故买「一天」的 costs[0] 最省钱。
- 第 9 - 19 不需要出门,则不用买
- 第 8 需要出门,需要买几天?
- 往后(只需看往后30天)有出门的需求
- 决策1:买一天期,后面的不包
- 决策2:买七天期,包到第 8 + 7 - 1 天,第 8 + 7 天往后的不包
- 决策3:买三十天期,包到第 8 + 30 - 1 天,第 8 + 30 天往后的不包
- 可见,决策3 包三十天期的话,第 20 可不用花钱
- 往后(只需看往后30天)有出门的需求
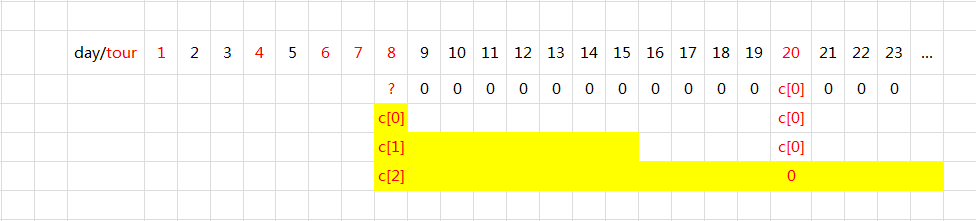
- …
- 抽象,定义状态:dp[i] 为第 i 天开始,累计所需最小费用
dp[i] = min(决策1, 决策2, 决策3); = min(c[0] + 1天后不包, c[1] + 7天后不包, c[2] + 30天不包); = min(c[0] + dp[i + 1], c[1] + dp[i + 7], c[2] + dp[i + 30]);

📝题解
int mincostTickets(vector<int>& days, vector<int>& costs) {
int len = days.size();
int dp[400] = {0};
for (int d = days[len-1], i = len-1; d >= days[0]; --d){
if (d == days[i]){
dp[d] = min(costs[0]+dp[d+1], costs[1]+dp[d+7]);
dp[d] = min(costs[2]+dp[d+30], dp[d]);
--i;
}
else dp[d] = dp[d+1];
}
return dp[days[0]];
}
