CC BY 4.0(除特别声明或转载文章外)
📝题目
给你一个列表 nums ,里面每一个元素都是一个整数列表。请你依照下面各图的规则,按顺序返回 nums 中对角线上的整数。
示例 1:
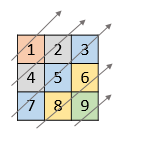
输入:nums = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,4,2,7,5,3,8,6,9]
示例 2:
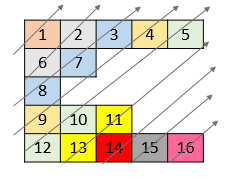
输入:nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出:[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]
示例 3:
输入:nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
输出:[1,4,2,5,3,8,6,9,7,10,11]
示例 4:
输入:nums = [[1,2,3,4,5,6]]
输出:[1,2,3,4,5,6]
提示:
· 1 <= nums.length <= 10^5
· 1 <= nums[i].length <= 10^5
· 1 <= nums[i][j] <= 10^9
nums 中最多有 10^5 个数字。
📝思路
因为矩阵不是完整填充的,所以不能直接遍历。考虑到是顺着对角线的同一方向,那么x+y就是相等的且次序一致,那么可以按照x+y去分类,建立一个二维数组ans[i] [j],i表示(x+y),然后正常遍历这个nums,每遍历到一个元素,看看它的x+y,把它丢到ans[x+y]中。
对角线遍历的另一种设定👉LeetCode-498 对角线遍历。
📝题解
vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
vector<int> result;
int row = nums.size();
vector<vector<int>> arr;//[i+j][count]
arr.resize(1e5);
int max = 0;
for (int i = 0; i < row; ++i){
int column = nums[i].size();
for (int j = 0; j < column; ++j){
arr[i+j].push_back(nums[i][j]);
}
max = column > max ? column : max;
}
for (int i = 0; i < row+max; ++i){
while (!arr[i].empty()){
result.push_back(arr[i].back());
arr[i].pop_back();
}
}
return result;
}
